I started working on this post about a month ago, but then proceeded to get side-tracked. I've been advised to write posts that contain less text, but this one was mostly written already, so I decided to finish it as is. Subsequent posts will more than likely contain less text.
--------------------------------------------------------------------------------------------------------------------------------
So I started delving into SURYA by actually reading the first few sections of the users' guide. Some things I've learned so far:
--------------------------------------------------------------------------------------------------------------------------------
So I started delving into SURYA by actually reading the first few sections of the users' guide. Some things I've learned so far:
- The code can run from a specified initial state if the variable "irelax" is set to 1 and a file "init.dat," which can be a renamed final.dat from a previous run, is provided. If irelax is set to 0, the code runs after generating its own initial state.
- The code runs in a region divided into a grid of r, θ values. By default this grid is 129-by-129. The region is given by 0.55 < r/R < 1 and 0 < θ < π. This means the step sizes between grid points are (3.48837x10-3)*R and π/129. Note that since we're working on (half of) a 2-D slice of a sphere, the further out from the center we are, the larger the area taken up by a grid block.
- The code runs in length units of 1010 cm (so R = 6.96), and time units of 108 sec (so 1 yr = 0.315).
At this point I think I've introduced enough of the code to start talking about some of the output files. Let's start with "run.dat." This file has 6 columns, and sorting through the code and the handy table of how quantities are represented (in the users' guide) one can determine that, respectively, columns 1 through 6 are time (in code units), B(r = 0.707R, θ = 74π/129), B(0.703R, 74π/129), B(0.707R, 54π/129), A(0.969R, 122π/129), and A(0.969R, 6π/129). I've been told that the units on B are 105 G, but I haven't seen this stated explicitly in the documentation or the code yet. These are the toroidal field at the bottom of the convection zone and a little ways south of the equator; toroidal field in the tachocline, again a little south of the equator; toroidal field at the bottom of the convection zone, just north of the equator (about as far north as the previous two values were south); the poloidal field just under the photosphere, close to the south pole; the poloidal field just under the photosphere, close to the north pole.
Another output file is "final.dat" This file has 4 columns: θ, r, A(r,θ)*r*sin(θ), and B(r,θ). Contours of column 3 yield the distribution of the poloidal field, and repeating the process with column 4 gives you the toroidal field.
Included with the code were some prepackaged MATLAB files that generate plots of various quantities. Most of these have names that suggest what quantity they plot, and they do so by reading in a .dat file, extracting the relevant columns, passing the necessary information to a similarly-named file (foo.m talks to fooplot.m) which makes regularly-spaced grids and/or pretty axes and specifies the type of plot (usually latitude vs. time or an r-θ plot). Some of this functionality I was already familiar with, but that was frequently not the case. Why is that?
In addition to learning the ins and outs of SURYA, I also face the problem of having little facility (in my opinion) with MATLAB. I'm going to attempt to cement some of the knowledge I've acquired recently, rather than just finding what I need when I need it and always referring to that instance when I need to perform a similar task. Unfortunately for the reader, that means I'm going to start explaining things as I understand them.
I promised to provide you guys with pictures, but I've been busy talking about how the pictures will be made instead of just, you know, putting them in. Seriously, they're coming.
Before I say anything else, let me introduce the help command. Typing "help nuisancecommand" will bring up a whole bunch of info about the command "nuisancecommand," including its syntax. I find how useful this is will vary from command to command. There is usually a link to the topic in the help browser at the bottom of the help entry, and I find this varies in usefulness as well. If neither of these is helping (and you've already tried a google search that didn't help either), your best bet is to try using the command on some non-crucial, trial arguments until you feel you understand its behavior. In fact, you should probably do that anyway.
I'm going to explain some array size commands so that I don't have to break up whatever flow might accidentally end up existing in the text later: Let's use a 1-by-n array (an n-element row vector), X, an m-by-1, array (an m-element column vector), Y, and an m-by-n array (a matrix or 2nd rank tensor) T.
The pcolor command creates a "checkerboard" plot based on the inputs it is given. With matrices x and y and a resultant function of x and y, z ( z = f(x,y) ):
pcolor(x,y,z)
will basically meshgrid x and y and plot a colored surface to represent the value of z. The resulting plot will have obvious grids and is an example of shading('faceted'). Typing in shading('flat') will remove the grids and shading('interp') will blend the coloring a little better by averaging values from the surrounding grid points at a given location (all this is covered in the help entry). Typing colorbar will place a colorbar outside and to the right of the plot. Ways to change the default positioning are covered in the help for colorbar.
Similar to pcolor is the surface command, but surface allows specification of a viewing angle, while pcolor is from directly overhead.
Also similar to pcolor is the contour command, but it only draws contours at levels that can be chosen automatically by MATLAB:
contour(x,y,z)
or by the user, let's say at values of z that correspond to the entries in the vector c:
contour(x,y,z,[c]).
An arbitrary two-element vector that receives the output from contour(x,y,z,[c]) can be used to label the contours. I'm going to use a semicolon on the first line this time--it suppresses the output:
[stuff1, stuff2] = contour(x,y,z,[c]);
clabel(stuff1, stuff2)
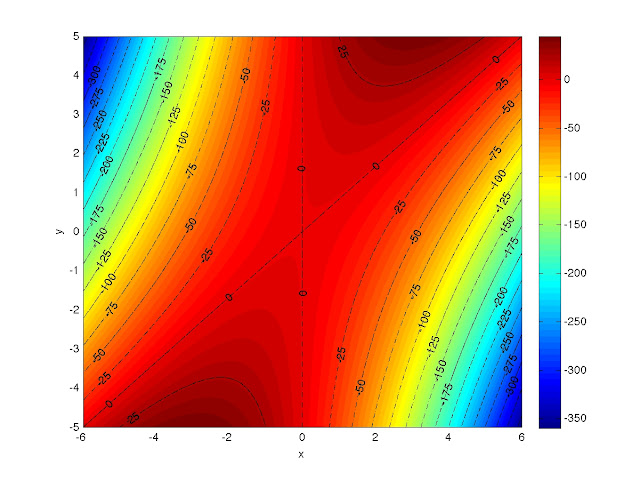
If you use the hold commands I mentioned before and play with the line coloring/style options (type "help plot"), you can get things that look like this:
Now, how did I get the picture out of MATLAB? MATLAB will save images (and probably other things) using the command print.
print -depsc 'filename.eps'
The "-depsc" is a flag that says save as a color (the "c") eps file (the "eps")--the ".eps" I put on the end of the filename isn't necessary. I also didn't need the single quotes around "filename.eps". To clarify
print -depsc filename
would have produced the same output.
The "d" part of the flag seems to be compulsory. The file will be saved as "filename.eps" in whatever directory MATLAB is currently working. You could change that by throwing around some UNIX file tree stuff beforehand. For example, ~/matlab_plots/filename.eps would put filename.eps into a directory matlab_plots. The directory matlab_plots would be a subdirectory of the user's home directory. I'm not planning on explaining any more "basic" UNIX than I just did. Some other flags are -dtiff, which saves as a .tiff, -dpng, which saves as a .png, -dps, which saves as a .ps, -djpeg (I assume you've noticed the pattern). The -djpeg flag can take a numerical argument right after it that specifies the quality of the file. A 0% quality file looks like this:
and a 100% quality file looks like this:
Those two plots are pcolor's of the example function I used for the contour plot. They were saved with the commands
print -djpeg0 crappy_example
and
print -djpeg100 full_example
One command that I came across while looking up things for this post is subplot. It looks like it will be VERY useful in the future, but I have yet to read through its help file or start experimenting with it. I find that what helps me most is knowing that a command that does what I'm trying to do already exists. At the very least, it'll save me some time doing a Google search. Another time, subplot, another time.
As I mentioned in the caption for the first picture, I plan on doing a walk-through of how I made the contour plot for the next blog entry. It'll probably have the same style as this entry, as they were originally meant to be the same post, but this one is turning into a mammoth already.
After that, the plan is for a post that shows the output from the plot routines that came along with SURYA and thereafter things will probably take on a "look what I did" as opposed to "look how I did this" feeling.
I promised to provide you guys with pictures, but I've been busy talking about how the pictures will be made instead of just, you know, putting them in. Seriously, they're coming.
Before I say anything else, let me introduce the help command. Typing "help nuisancecommand" will bring up a whole bunch of info about the command "nuisancecommand," including its syntax. I find how useful this is will vary from command to command. There is usually a link to the topic in the help browser at the bottom of the help entry, and I find this varies in usefulness as well. If neither of these is helping (and you've already tried a google search that didn't help either), your best bet is to try using the command on some non-crucial, trial arguments until you feel you understand its behavior. In fact, you should probably do that anyway.
I'm going to explain some array size commands so that I don't have to break up whatever flow might accidentally end up existing in the text later: Let's use a 1-by-n array (an n-element row vector), X, an m-by-1, array (an m-element column vector), Y, and an m-by-n array (a matrix or 2nd rank tensor) T.
- size: will return the number of rows and the number of columns. The command size(X) would return [1 n], size(Y) would return [m 1] and size(T) would return [m n].
- numel: will return the number of elements in an array (the number of rows multiplied by the number of columns). The command numel(T) would return the number m*n, even if one of the elements is 0.
- length: will return the larger of the dimensions: it is basically max(size( )). I assume you can infer what the max( ) command does. The command length(T) will return the larger of m and n.
The command meshgrid will create a grid of points based on the arguments you give it. For example, lets say:
[u,v] = meshgrid(a,b).
For my purposes, a and b will be row vectors with different dimensions. What this command does is produce two matrices, u and v. The matrix u has numel(b) rows, all of which are the vector a. The dimensions of u are numel(b)-by-numel(a). The matrix v has numel(a) columns, all of which are the transpose of the vector b. The dimensions of v are numel(a)-by-numel(b). If you need to make the vectors a and b between some given boundaries and know how many data points you need the boundaries, the linspace command will probably come in handy:
linspace(c,d) will return a vector of 100 evenly spaced points between the numbers c and d.
linspace(c,d,n) will return a vector of n evenly spaced points between the number c and d.
Either of those things could be accomplished with colon notation (type "help colon"), but linspace might be easier in some instances.
linspace(c,d) will return a vector of 100 evenly spaced points between the numbers c and d.
linspace(c,d,n) will return a vector of n evenly spaced points between the number c and d.
Either of those things could be accomplished with colon notation (type "help colon"), but linspace might be easier in some instances.
The reshape command takes a given array and rearranges it into an array with the given dimensions:
q = reshape(xi,M,N) will take the array "xi" and produce an array that is M rows-by-N columns. The first column will be the first M entries of xi, the second column will be the second M entries, and so on. MATLAB refers to this as taking the elements of xi "columnwise."
Before I forget to mention them, here are some basic plotting commands and functionality:
Before I forget to mention them, here are some basic plotting commands and functionality:
- The command hold on will tell MATLAB that it should draw whatever you ask for next on top of the figure in which you are currently working. The command hold off will turn this behavior off.
- The command figure() (or just figure) will open a new plot figure. Typing figure(k) will tell MATLAB that the next series of commands should affect figure k--sometimes I find this easier than trying to find the figure I want and give it window focus when I have multiple figures open. If you're looking at a figure window and just start typing, MATLAB will shift focus back to the command window, so at least you don't have to find the right figure and then find the command window again.
The pcolor command creates a "checkerboard" plot based on the inputs it is given. With matrices x and y and a resultant function of x and y, z ( z = f(x,y) ):
pcolor(x,y,z)
will basically meshgrid x and y and plot a colored surface to represent the value of z. The resulting plot will have obvious grids and is an example of shading('faceted'). Typing in shading('flat') will remove the grids and shading('interp') will blend the coloring a little better by averaging values from the surrounding grid points at a given location (all this is covered in the help entry). Typing colorbar will place a colorbar outside and to the right of the plot. Ways to change the default positioning are covered in the help for colorbar.
Similar to pcolor is the surface command, but surface allows specification of a viewing angle, while pcolor is from directly overhead.
Also similar to pcolor is the contour command, but it only draws contours at levels that can be chosen automatically by MATLAB:
contour(x,y,z)
or by the user, let's say at values of z that correspond to the entries in the vector c:
contour(x,y,z,[c]).
An arbitrary two-element vector that receives the output from contour(x,y,z,[c]) can be used to label the contours. I'm going to use a semicolon on the first line this time--it suppresses the output:
[stuff1, stuff2] = contour(x,y,z,[c]);
clabel(stuff1, stuff2)
If you use the hold commands I mentioned before and play with the line coloring/style options (type "help plot"), you can get things that look like this:
Now, how did I get the picture out of MATLAB? MATLAB will save images (and probably other things) using the command print.
print -depsc 'filename.eps'
The "-depsc" is a flag that says save as a color (the "c") eps file (the "eps")--the ".eps" I put on the end of the filename isn't necessary. I also didn't need the single quotes around "filename.eps". To clarify
print -depsc filename
would have produced the same output.
The "d" part of the flag seems to be compulsory. The file will be saved as "filename.eps" in whatever directory MATLAB is currently working. You could change that by throwing around some UNIX file tree stuff beforehand. For example, ~/matlab_plots/filename.eps would put filename.eps into a directory matlab_plots. The directory matlab_plots would be a subdirectory of the user's home directory. I'm not planning on explaining any more "basic" UNIX than I just did. Some other flags are -dtiff, which saves as a .tiff, -dpng, which saves as a .png, -dps, which saves as a .ps, -djpeg (I assume you've noticed the pattern). The -djpeg flag can take a numerical argument right after it that specifies the quality of the file. A 0% quality file looks like this:
 |
| A reproduction of z = 6*x*y - 5*x2 at the poorest quality possible. |
 |
| A reproduction of z = 6*x*y - 5*x2 at the highest quality possible. |
print -djpeg0 crappy_example
and
print -djpeg100 full_example
One command that I came across while looking up things for this post is subplot. It looks like it will be VERY useful in the future, but I have yet to read through its help file or start experimenting with it. I find that what helps me most is knowing that a command that does what I'm trying to do already exists. At the very least, it'll save me some time doing a Google search. Another time, subplot, another time.
As I mentioned in the caption for the first picture, I plan on doing a walk-through of how I made the contour plot for the next blog entry. It'll probably have the same style as this entry, as they were originally meant to be the same post, but this one is turning into a mammoth already.
After that, the plan is for a post that shows the output from the plot routines that came along with SURYA and thereafter things will probably take on a "look what I did" as opposed to "look how I did this" feeling.
No comments:
Post a Comment